Cake Puzzle is a Reverse Engineering challenge from the CakeCTF 2023.


Figure 1 - Cake Puzzle challenge

The challenge gives us a compressed file with the binary for the compiled program which we are supposed to reverse engineer. It also gives us a Netcat command to connect to their server: nc others.2023.cakectf.com 14001.

Solution

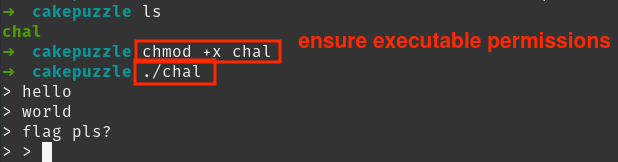
The first step I took was to run the file with executable permissions. We are prompted to insert an input which seems to be subsequent, as it’s demonstrated in figure 2.


Figure 2 - Execution of the binary “chal”

I decided to use Ghidra to perform static analysis on the executable.


Figure 3 - Import of “chal” to Ghidra

main() function

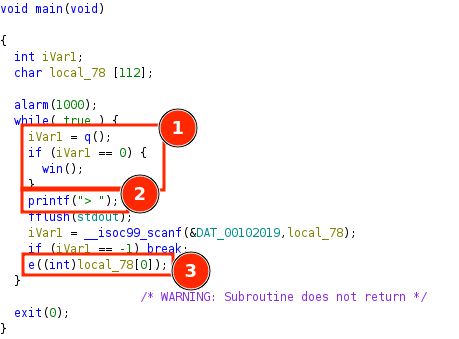
Upon analyzing the symbols and decompiling the code we can search for the main() function. The goal of the research is to understand what the program is doing in its integrity, so it’s common and best practice to rename functions and variables as we advance further.

As we can see in figure 4, there are a few key points to notice:

There is an infinite loop that is checking the value returned by the q() function. At first glance, if the returned value is 0, then we reach the win() function, which means win() probably returns us the flag, as we will confirm later.
We can identify the input prompt and the variable storing the input.
The first character of the input, local_78[0], is given to the e() function.


Figure 4 - main() function

q() function

Let’s now take a look at the q() function in depth:


Figure 5 - q() function

Notice these instructions basically represent a pair of nested for loops, iterating local_c from 0 to 2 (outer loop) and local_10 from 0 to 2, for each local_c (inner loop).
Inside the inner loop, two conditions are being verified. In order to reach our win() function we need to ensure the loops reach their end without ever one of these conditions being met. We are introcuded to the varibale M which appears to be a matrix. The conditions seem to be accessing and comparing values of the matrix. The *4 in the code is used for pointer arithmetic, specifically to account for the size of the data type being pointed to. In this case, the data type is int, which typically occupies 4 bytes in memory. This usage of *4 aligns with the assumption that each element in the matrix is an integer.

win() function

By looking at the win() function, we confirm that it, indeed, returns the flag.


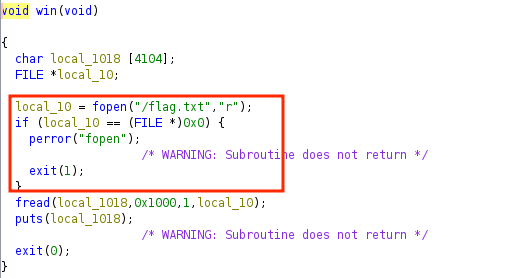Figure 6 - win() function

e() function

Now, we can assume that our input is somehow modifying the matrix M until the q() function returns 0. Let’s look at the function e() and understand what it’s doing with the input.


Figure 7 - e() function

Function s() is being called. Based on the context of the problem, that is becoming clearer, we’ll assume local_c and local_10 are variables representing rows and columns of the matrix M. s() is addressed in the next section.
Our input is being compared to a set of characters to perform different operations. The possibilities are U, R, D, L which are probably moves UP, RIGHT, DOWN and LEFT, respectively, which will affect the values in the matrix.
We conclude that we are dealing with a 4 by 4 matrix of integer values, since before performing f(), the program is making sure indexes out of bounds are not accessed.

s() function

This function iterates trough all the possible indexes of the 4 by 4 matrix, and assigns param1 and param2 the indexes where the value is 0.


Figure 8 - s() function

f() function

Finally, the f() function swaps the values of the matrix using the XOR swap algorithm, which is a very efficient way of swapping two values between variables. Figure 10 is a brief representation on how the algorithm works.


Figure 5 - f() function


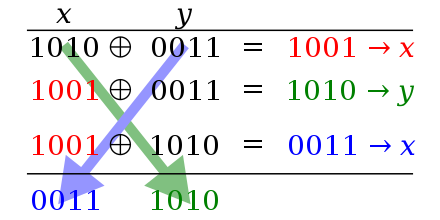Figure 10 - XOR swap algorithm

Interpretation

It is now clear that this program represents a very well known puzzle: the 15 Puzzle!


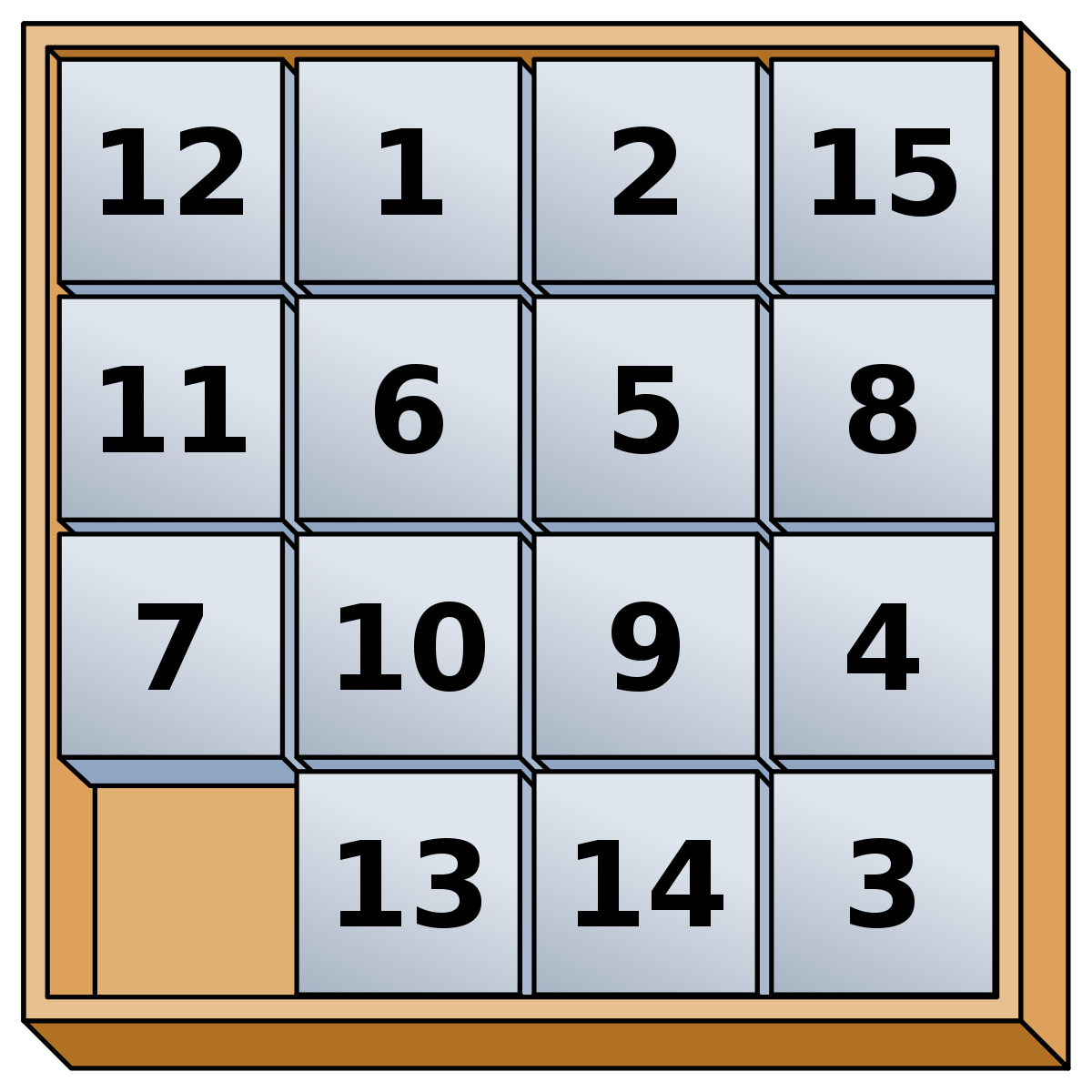Figure 11 - Unsolved 15 Puzzle


Figure 12 - Solved 15 Puzzle

We have a 4 by 4 matrix, representing our board and the 0 value representing the empty space. Furthermore, the moves U, R, D, L represent the sliding of the tiles and the win condition represents a goal state we want to reach in order to retrieve the flag. Specifically, the condition is the same as the one from the classic puzzle: for each value of the matrix, it has to be inferior than the value below it and on its right. Let’s change the names of the functions and variables accordingly to facilitate reading the decompiled code.


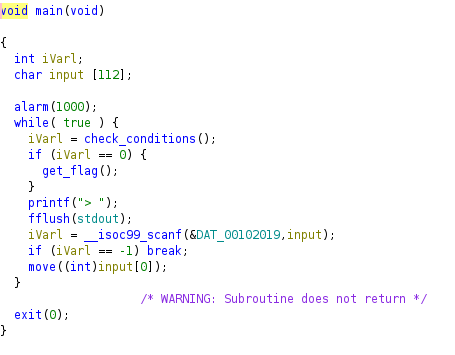Figure 13 - New main() function


Figure 14 - New q() function


Figure 15 - New e() function


Figure 16 - New s() function

Solving with IDA*

The approach to solve the problem is using a 15 Puzzle solver that uses Artificial Intelligence algorithms like IDA* (Iterative deepening A*). These types of solvers need to be given the initial state (initial matrix) of the 15 Puzzle and the goal state (goal matrix).

The initial state of the matrix M can be found in memory before even executing the program using GDB like so:


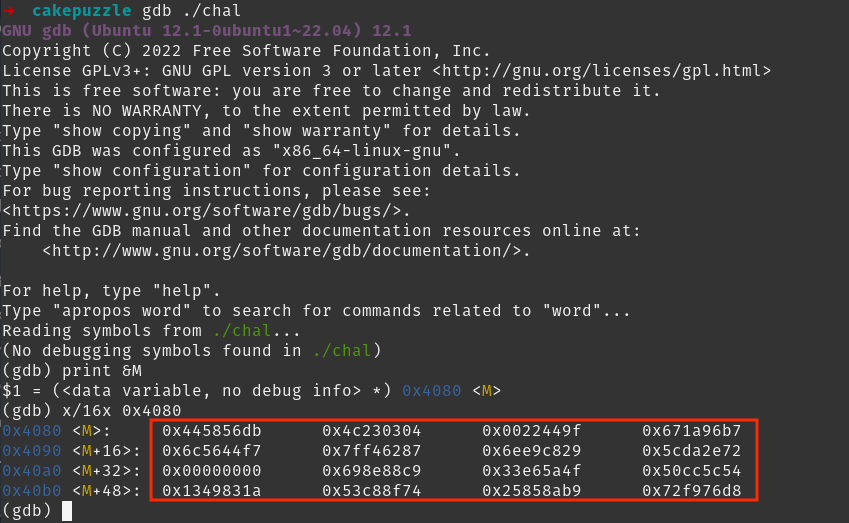Figure 17 - Matrix M found using GDB

Our goal is to have a matrix of numbers from 0 to 15, representing the initial state. Unfortunately, the values inside the matrix are all in base 16 (hexadecimal). So, we have to convert the values into decimal. We end up with a matrix with very large integers and the empty space, 0. Since the conditions only care about the relative inferiority/superiority of the values, we can map them to numbers from 0 to 15 based on it. We end up with this 4 by 4 matrix:


Figure 18 - Initial state

We can now give this initial state to the solver, along with a goal state, and it will try to find the optimal solution. There is, however, a small nuance: not all puzzles are solvable. As stated by Johnson & Story (1879):

“Johnson & Story (1879) used a parity argument to show that half of the starting positions for the n puzzle are impossible to resolve, no matter how many moves are made. This is done by considering a function of the tile configuration that is invariant under any valid move and then using this to partition the space of all possible labelled states into two equivalence classes of reachable and unreachable states. The invariant is the parity of the permutation of all 16 squares plus the parity of the taxicab distance (number of rows plus number of columns) of the empty square from the lower right corner. This is an invariant because each move changes both the parity of the permutation and the parity of the taxicab distance. In particular, if the empty square is in the lower right corner, then the puzzle is solvable if and only if the permutation of the remaining pieces is even. “

Our initial state falls exactly into that category, as it’s shown in figure 18.


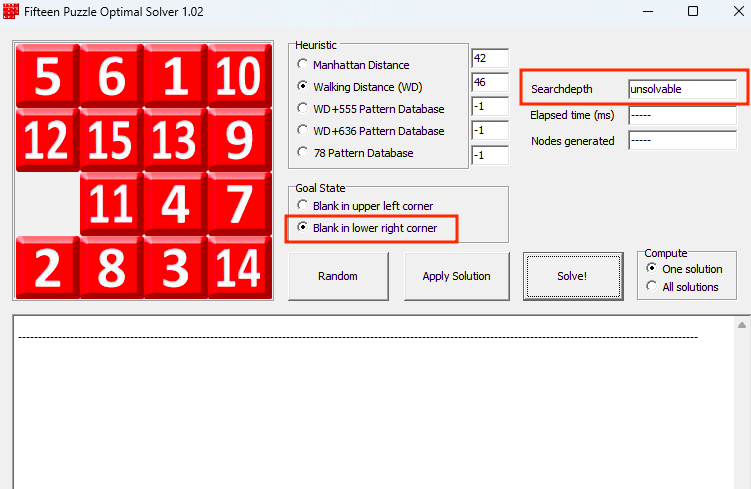Figure 19 - Unsolvable puzzle

However, this is only true for the standard goal state of the puzzle (figure 12). The rules change depending on the goal state, which means we can find a more appropriate goal state that makes the puzzle solvable and that still allows all the victory conditions to be met!

Indeed, if we choose another common goal state where the empty space is in the top left corner, instead of the bottom right one, then we reach a solution. Here is a representation of that goal state:


Figure 20 - Goal state


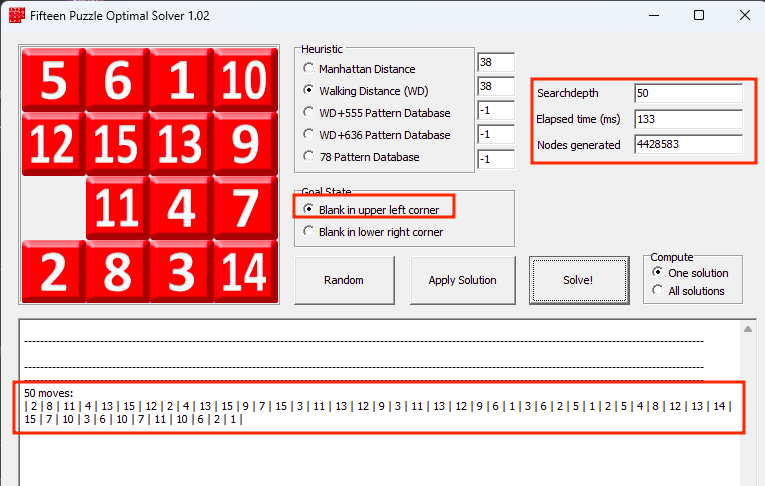Figure 21 - Solution to reach the goal state

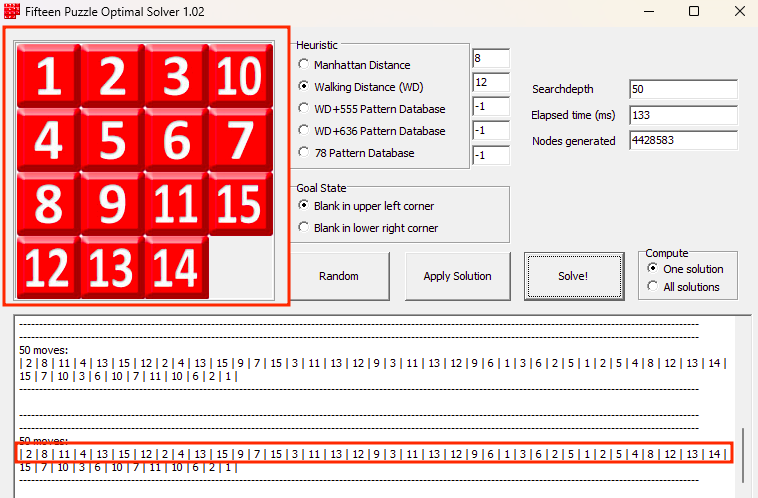
After indicating the solver to use these states, we are given a possible (optimal) solution:

All that’s left is to translate the moves into U, R, D, L and subsequently give them to the input prompt after connecting to the CakeCTF server and port indicated with the following command: nc others.2023.cakectf.com 14001

Possible solution: D R U R U L L D R R U R D L D L U U R D D L U U U R D L L U R D L D D R R R - CakeCTF{wh0_at3_a_missing_pi3c3_0f_a_cak3}


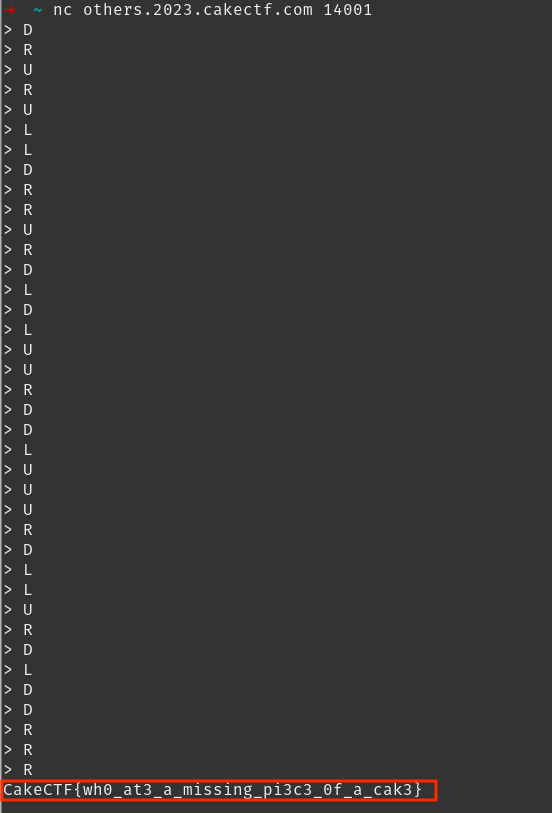Figure 22 - Solution to reach the goal state

Figure 22 shows the state of the matrix after performing the moves from the solution. The conditions ended up being met before we reached the defined goal state (only 38 moves). This comes to show that there are more than one possible final states so that the conditions are met, since there is no specification for where the number and empty space should be, exactly. We reached the flag before completing all the moves given by the solver because the conditions were met before we reached our defined goal state (figure 19). Note that the conditions didn’t allow the check of the values below and on the right if one of them didn’t exist.


Figure 23 - State of the matrix upon retrieval of the flag

Challenge and writeup by: João Gonçalo de Faria Melo

5h13d4